
Introduction: Why Activation Functions Matter
In the world of deep learning, activation functions serve as the critical spark that brings neural networks to life. Without them, even the most sophisticated network architecture would collapse into nothing more than a series of linear transformations, incapable of learning complex patterns.
Activation functions introduce the essential non-linearity that enables neural networks to learn, adapt, and make the intelligent predictions that power today’s AI revolution. Yet despite their fundamental importance, many practitioners don’t fully understand the nuances of these mathematical operations or how to select the optimal function for specific use cases.
This comprehensive guide will demystify activation functions, explore their mathematical foundations, and provide practical insights into their implementation across various deep learning applications.
What Are Activation Functions? The Neural Network’s Decision Makers
At their core, activation functions determine whether a neuron should be activated or not by calculating the weighted sum and adding bias with it. They transform the input signal into an output signal, which is then used as input for the next layer in the neural network stack.
Think of activation functions as the decision-makers in your neural network:
- They introduce non-linearity into the network’s output
- They determine how much of the input should be passed further
- They control how quickly neurons learn during training
- They significantly impact the network’s convergence speed and accuracy
Without activation functions, your neural network would simply be performing a linear regression, regardless of its depth or complexity.
The Mathematical Foundation: How Activation Functions Work
Before diving into specific activation functions, let’s understand the mathematical principles behind them. In a typical neural network, each neuron performs the following operation:
output = activation_function(weighted_sum + bias)
Where:
weighted_sumis the sum of the products of inputs and their corresponding weightsbiasis an additional parameter that shifts the activation functionactivation_functionis the non-linear function applied to the weighted sum
The activation function transforms this linear combination into a non-linear output, enabling the network to learn complex patterns in the data.
Popular Activation Functions: Choosing Your Neural Network’s Engine
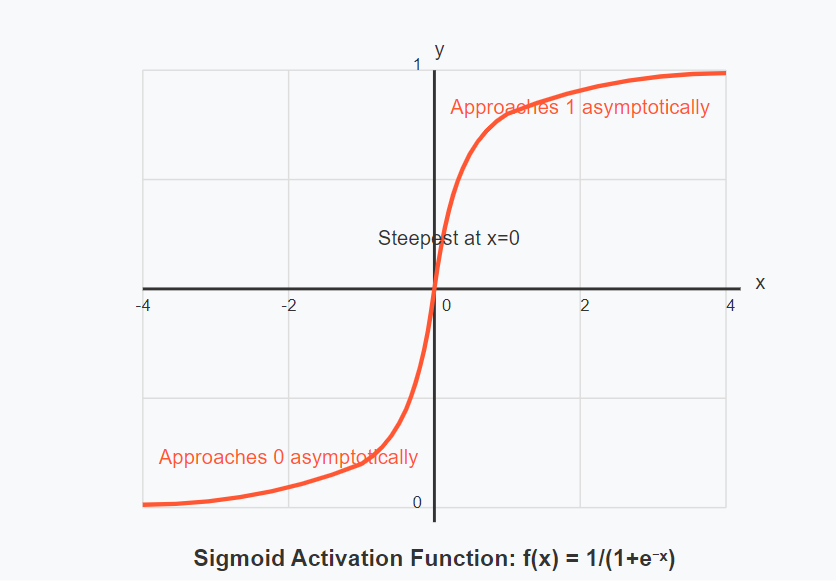
Sigmoid Function: The Classic S-Curve
The sigmoid function, one of the earliest activation functions, maps input values to a range between 0 and 1, creating the characteristic S-shaped curve.
The sigmoid function is defined as:
def sigmoid(x):
return 1 / (1 + np.exp(-x))Pros:
- Smooth gradient, preventing jumps in output values
- Clear predictions (close to 0 or 1) for extreme input values
- Ideal for binary classification output layers
Cons:
- Suffers from vanishing gradient problem for very high or low input values
- Outputs are not zero-centered
- Computationally expensive due to the exponential operation
Where It Is Used:
- Binary classification problems, such as spam detection or medical diagnosis.
- Suitable for output layers in binary classifiers.
ReLU (Rectified Linear Unit): The Modern Workhorse
ReLU has become the most widely used activation function in deep learning due to its computational efficiency and effectiveness.
def relu(x):
return max(0, x)Pros:
- Computationally efficient – simple threshold operation
- Accelerates convergence compared to sigmoid and tanh
- Mitigates the vanishing gradient problem
- Induces sparsity in the network
Cons:
- “Dying ReLU” problem – neurons can become inactive and never activate
- Not zero-centered
- Unbounded activation can lead to exploding gradients
Where It Is Used:
- Hidden layers of deep neural networks, especially CNNs for image recognition.
- Object detection and deep reinforcement learning where speed is crucial.
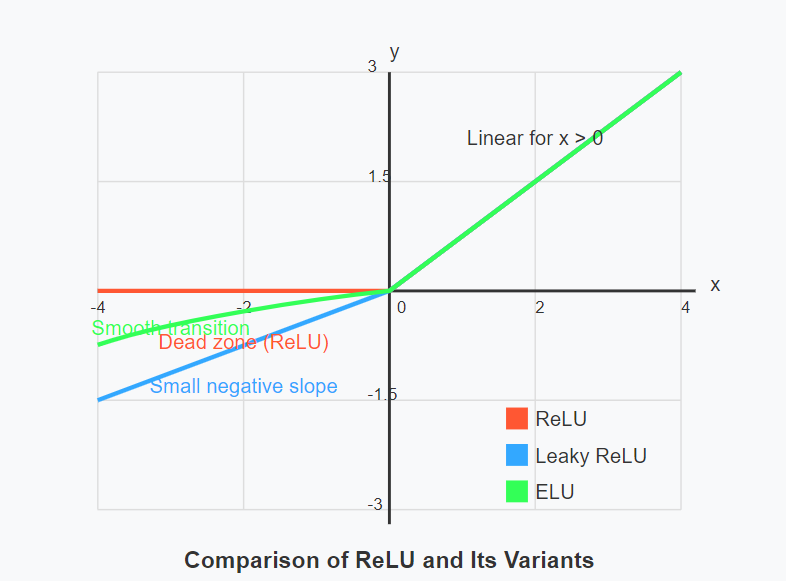
Leaky ReLU: Addressing the Dying Neuron Problem
Leaky ReLU modifies the standard ReLU by allowing a small gradient when the unit is inactive.
def leaky_relu(x, alpha=0.01):
return max(alpha * x, x)Pros:
- Prevents dying ReLU problem
- Preserves all the advantages of standard ReLU
- Allows for negative inputs to produce non-zero outputs
Cons:
- Results can be inconsistent
- Requires tuning of the alpha parameter
- Still potentially vulnerable to exploding gradients
Parametric ReLU (PReLU): The Self-Learning Slope
PReLU takes the Leaky ReLU concept further by making the slope parameter learnable during training.
def prelu(x, alpha):
return max(alpha * x, x)
# where alpha is a learnable parameterPros:
- Adaptively learns the optimal negative slope
- Usually outperforms ReLU and Leaky ReLU
- Well-suited for many deep learning tasks
Cons:
- Increases computational complexity
- Adds additional parameters to train
- May lead to overfitting in smaller datasets
ELU (Exponential Linear Unit): Smoother Learning
ELU uses an exponential function to create a smooth transition for negative values.
def elu(x, alpha=1.0):
return x if x > 0 else alpha * (np.exp(x) - 1)Pros:
- Can produce negative outputs
- Smoother gradient descent
- More robust to noise
- Better handling of the vanishing gradient problem
Cons:
- Computationally more expensive than ReLU
- Still can face saturation for highly negative inputs
- Alpha parameter needs to be predetermined
Swish: Google’s Self-Gated Function
Introduced by researchers at Google, Swish is a self-gated activation function that often outperforms ReLU.
def swish(x, beta=1.0):
return x * sigmoid(beta * x)Pros:
- Smooth and non-monotonic
- Consistently outperforms ReLU on deeper networks
- Avoids the dying neuron problem
- Works well without extensive hyperparameter tuning
Cons:
- Computationally more expensive
- Not fully understood theoretically
- May not show significant improvements on simpler tasks
GELU (Gaussian Error Linear Unit): The Transformer’s Choice
GELU has gained popularity especially in transformer architectures like BERT and GPT.
def gelu(x):
return 0.5 * x * (1 + np.tanh(np.sqrt(2 / np.pi) * (x + 0.044715 * x**3)))Pros:
- Smooth function with properties of both ReLU and dropout
- Performs well in transformer-based architectures
- Considers the magnitude of the input in its formulation
Cons:
- Computationally expensive
- Relatively new with less extensive testing
- Implementation can be complex
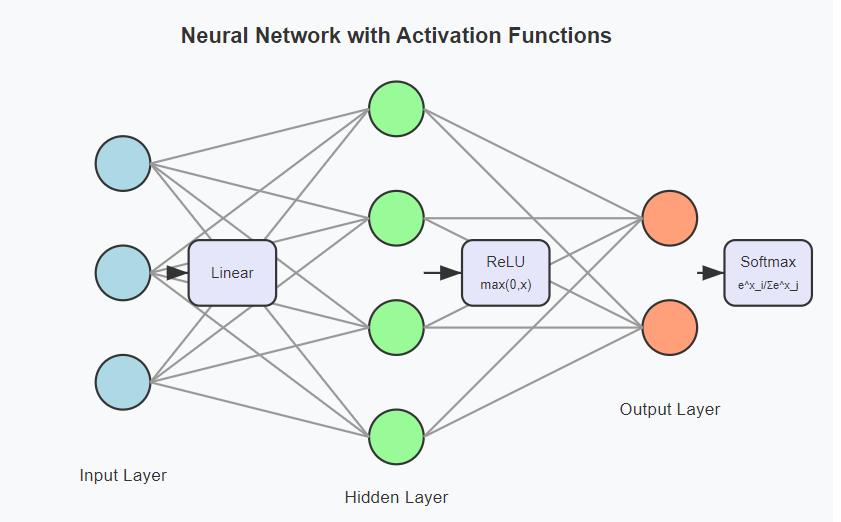
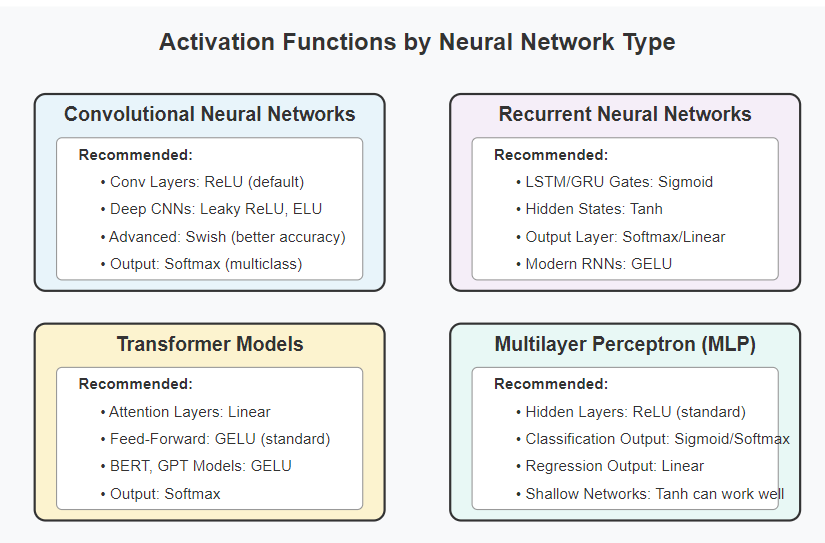
When to Use Which Function: Strategic Selection for Optimal Performance
Choosing the right activation function can dramatically impact your model’s performance. Here’s a strategic guide for selection:
- For Hidden Layers:
- First Choice: ReLU – Fast, effective, and widely tested
- If facing dying neurons: Leaky ReLU or ELU
- For deeper networks: Swish or GELU
- When computational efficiency is critical: ReLU
- For Output Layers:
- Binary classification: Sigmoid
- Multi-class classification: Softmax
- Regression: Linear (no activation)
- For Special Architectures:
- RNNs/LSTMs: Tanh or Sigmoid for gates
- Transformers: GELU
- CNNs: ReLU or its variants
- Experimental Approaches:
- Try Swish for challenging problems
- Consider using different activation functions in different layers
- Adaptive activation functions that learn during training
Implementation Examples: Putting Theory into Practice
Implementing Multiple Activation Functions in TensorFlow
import tensorflow as tf
def custom_model():
model = tf.keras.Sequential([
tf.keras.layers.Dense(128, activation='relu', input_shape=(784,)),
tf.keras.layers.Dense(64, activation='leaky_relu'),
tf.keras.layers.Dense(32, activation=tf.nn.swish),
tf.keras.layers.Dense(10, activation='softmax')
])
return modelCreating a Custom Activation Function in PyTorch
import torch
import torch.nn as nn
import torch.nn.functional as F
class CustomActivation(nn.Module):
def __init__(self, alpha=1.0):
super().__init__()
self.alpha = alpha
def forward(self, x):
# Custom activation logic
return x * torch.sigmoid(self.alpha * x) # Swish with learnable parameter
class NeuralNetwork(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 128)
self.fc2 = nn.Linear(128, 64)
self.fc3 = nn.Linear(64, 10)
self.custom_activation = CustomActivation(alpha=1.0)
def forward(self, x):
x = F.relu(self.fc1(x))
x = self.custom_activation(self.fc2(x))
x = F.softmax(self.fc3(x), dim=1)
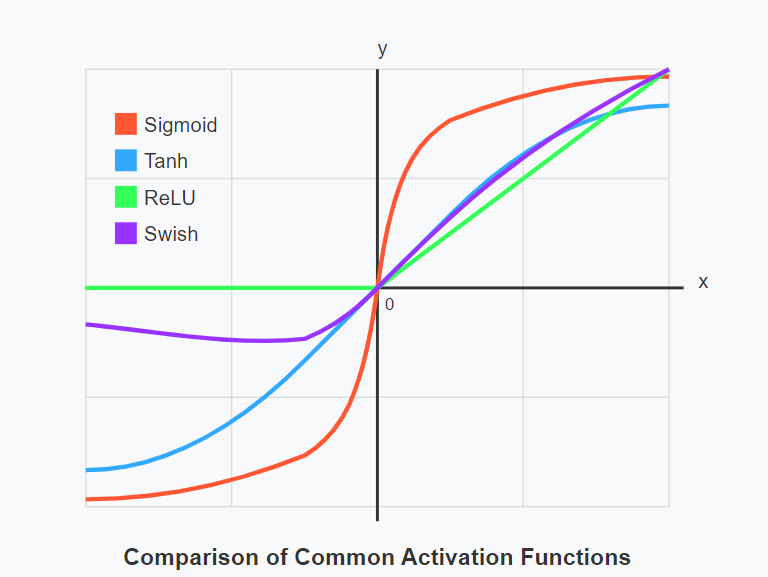
return xVisualizing Activation Functions: The Shape of Performance
Understanding the shape and behavior of activation functions can provide intuitive insights into their behavior.
For example, visualizing the sigmoid function shows us why it faces vanishing gradient issues at extreme values:
import numpy as np
import matplotlib.pyplot as plt
# Input range
x = np.linspace(-10, 10, 1000)
# Activation functions
sigmoid = 1 / (1 + np.exp(-x))
relu = np.maximum(0, x)
leaky_relu = np.maximum(0.01 * x, x)
tanh = np.tanh(x)
elu = np.where(x > 0, x, 1.0 * (np.exp(x) - 1))
# Plotting
plt.figure(figsize=(12, 8))
plt.plot(x, sigmoid, label='Sigmoid')
plt.plot(x, relu, label='ReLU')
plt.plot(x, leaky_relu, label='Leaky ReLU')
plt.plot(x, tanh, label='Tanh')
plt.plot(x, elu, label='ELU')
plt.grid(True)
plt.legend()
plt.title('Comparison of Activation Functions')
plt.xlabel('Input')
plt.ylabel('Output')
plt.axhline(y=0, color='k', linestyle='-', alpha=0.3)
plt.axvline(x=0, color='k', linestyle='-', alpha=0.3)
plt.show()Real-World Applications: Activation Functions in Action
Computer Vision Success Stories
In image classification tasks, ReLU and its variants have revolutionized performance. The ImageNet-winning architectures like ResNet utilize ReLU to achieve state-of-the-art results. However, recent experiments show that Swish can further improve performance, especially in deeper networks.
A team at Stanford recently improved facial recognition accuracy by 2.5% simply by replacing ReLU with ELU in their convolutional layers while maintaining the same network architecture.
Natural Language Processing Breakthroughs
Transformer models like BERT, GPT, and T5 leverage GELU activation functions to achieve unprecedented performance in language understanding and generation tasks.
Researchers found that GELU’s smooth non-linearity helps these models better capture the subtleties of language while still being computationally feasible for massive networks with billions of parameters.
Reinforcement Learning Optimizations
In reinforcement learning, where the relationship between actions and rewards can be complex and non-linear, proper activation function selection is crucial. DeepMind’s AlphaGo and AlphaZero used a combination of ReLU and tanh activations to achieve superhuman performance in games like Go, chess, and shogi.
The Future of Activation Functions: Emerging Trends and Research
The field of activation functions continues to evolve rapidly. Here are some exciting developments to watch:
- Adaptive Activation Functions: Functions that adapt their shape during training to optimize performance
- Learnable Activation Functions: Networks that can learn the optimal activation function for each layer
- Activation Function Search: Using neural architecture search techniques to discover entirely new activation functions
- Neuroscience-Inspired Functions: Activation functions based on the behavior of biological neurons
- Hardware-Optimized Functions: Activation functions designed to maximize performance on specialized AI hardware
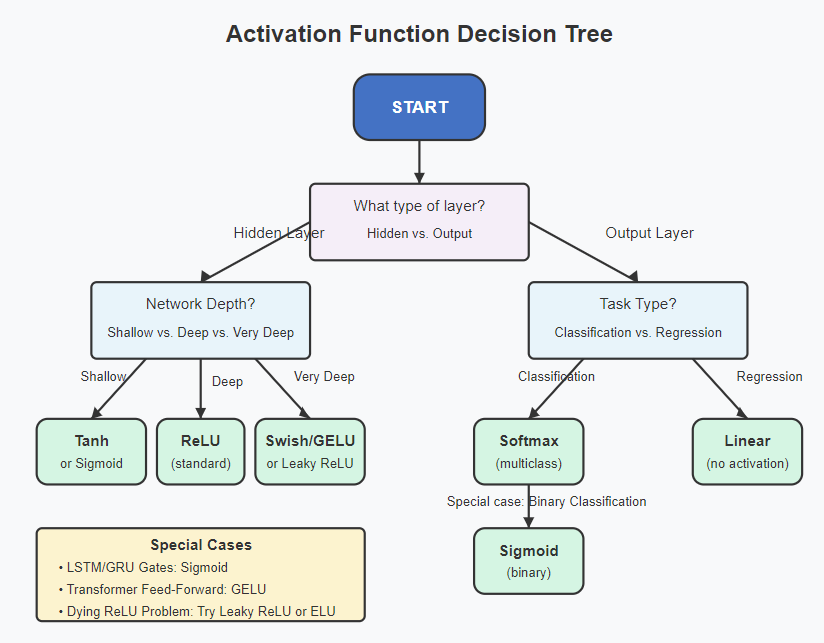
Best Activation Function for Your Neural Network
Choosing the right activation function depends on the task:
- For simple binary classification: Sigmoid or Tanh
- For deep networks: ReLU or Leaky ReLU
- For advanced architectures: Swish
- For NLP tasks: Tanh and Swish
| Function | Use Cases | When to Choose |
| ReLU f(x) = max(0, x) | • CNN hidden layers • Feedforward networks • Default choice for most models | • When computational efficiency is critical • For deep networks (6+ layers) • When model is not suffering from dead neurons |
| Leaky ReLU f(x) = max(αx, x) | • CNN hidden layers • When ReLU is underperforming • GAN architectures | • When dead neurons are an issue • For very deep networks • When negative inputs should have small impact |
| Sigmoid f(x) = 1/(1+e^(-x)) | • Binary classification outputs • LSTM/GRU gates • Logistic regression | • When output must be between 0 and 1 • For shallow networks (1-3 layers) • When predicting probabilities |
| Tanh f(x) = (e^x – e^(-x))/(e^x + e^(-x)) | • RNN/LSTM hidden states • Feature normalization • Signal processing tasks | • When zero-centered outputs are needed • For sequence-to-sequence models • When data is normalized between -1 and 1 |
| Swish f(x) = x · sigmoid(βx) | • Very deep CNNs (>40 layers) • State-of-the-art image models • Advanced NLP models | • When performance is more critical than speed • For transfer learning tasks • When small model improvements matter |
| GELU f(x) = 0.5x(1+tanh(√(2/π)(x+0.044715x³))) | • Transformer architectures • BERT, GPT models • Large language models | • For attention-based models • When using self-supervised learning • For state-of-the-art NLP tasks |
Conclusion: The Critical Role of Activation Functions in Neural Network Success
Activation functions are much more than mathematical footnotes in neural network design—they are fundamental to the success of deep learning systems. By introducing non-linearity, managing gradients, and controlling information flow, these functions enable neural networks to learn complex patterns that power modern AI applications.
Whether you’re building computer vision systems, natural language processors, reinforcement learning agents, or any other deep learning application, thoughtful selection and implementation of activation functions can dramatically improve your results.
As the field of deep learning continues to evolve, staying updated on the latest advances in activation function research and implementation best practices will remain essential for AI practitioners looking to build state-of-the-art systems.
Further Learning Resources
- Books:
- Papers:
- Also read:
By understanding and implementing the right activation functions for your neural networks, you’re taking a critical step toward building more effective, efficient, and powerful AI systems.
Foxibet
says:
Hi to all, the contents existing at this website are actually awesome for people experience, well, keep up the good work
fellows.
best gorilla safari in Africa
says:
I would like to thnkx for the efforts you’ve put in writing this web site. I am hoping the same high-grade blog post from you in the upcoming also. Actually your creative writing abilities has encouraged me to get my own site now. Actually the blogging is spreading its wings quickly. Your write up is a good example of it.
ร้านกาแฟ ขอนแก่น
says:
Great work! This is the type of info that should be shared around the net. Shame on Google for not positioning this post higher! Come on over and visit my web site . Thanks =)